A Ray Tracer - Part 1

Tags: C, Graphics, Mathematics, Programming, Ray Tracing

I've always been fascinated with computer graphics. One of the first things I learned to code when I was a kid was a ray tracer. It was a simple and straight-forward assembly implementation on an early home computer, but it taught me a lot about how computers deal with graphics and just programming in general and its connection to mathematics.

A couple of years ago, I decided to use ray tracing as the main theme of a course on C programming. More often than not, C programming courses tend to be dull installments of going over the various data types, the use of simple functions and program flow control, and of course arrays and pointers - without doing something useful. At the same time, the youth these days are so visually overloaded that printing "Hello world" 10 times in a loop to the console just doesn't speak to their imagination.

Little did I know during the course preparations how disconnect many young people (with very few exceptions) are when it comes to mathematics and its use. It's not so much that they can't memorise a mathematical formula, it is that they have no idea what they are memorising and what it can be used for. I highly recommend reading "A Mathematician's Lament" by Paul Lockhart to get an idea of the underlying issues.

Back to ray tracing. I want to write this down so it can be used as a reference by other people interested in the world of computer graphics. At the end of the story, you will have a simple ray tracer with which you can experiment and play, augment and dissect. I hope it may open a door which was closed before and which can help you to understand the link between mathematics and computer graphics the way that first ray tracer did for me. For this purpose, I tried to keep the math as simple as possible, and build from the ground up and verbose. Similarly, for the programming aspect, all you need to know is the basics of how to use a C compiler for your favorite platform. This way, I hope that everyone with a minimal mathematical background and limited programming skills can follow.

Ray tracing is exactly what the name says it is: tracing rays. Think of the pinhole camera which captures rays of light and projects them on a canvas. In ray tracing, we do the exact opposite: we shoot rays through the screen and find out where they end up. They might get reflected, cast shadows, etc. and end up at an object, light source, ... . When we do this for every pixel on the screen, we can determine the colour of each of them and create an image. In this way, we can depict a 3D scene on a 2D screen. The figure below taken from the Wikipedia article illustrates the concept. You might want to glance over some of the graphics in that article (and don't get scared of the math involved).

So, how do we express this concept into a programming language so that we can see some nice graphic when we're done. In a three dimensional space, each point is represented by three coordinates (x,y,z). These only make sense when we agree on an origin as well, let's keep it simple and have the origin at (0,0,0). The line connecting these two points, going from (0,0,0) to (x,y,z) is what is called a vector, in this case in three dimension.

In the C programming language, we can easily represent a vector using a struct as follows:

typedef struct{
      float x,y,z;
}vector;

Since we agreed on taking (0,0,0) as origin, the three values (x,y,x) of this struct represent the location of a point in 3 dimensional space with (0,0,0) as reference. Drawing a line from (0,0,0) to (x,y,z) forms the vector.

Now, let's take a ray. In the figure above, a ray which we shoot through the screen could end up hitting the sphere in the scene. Or it may not and miss the sphere altogether. We have to find a way to determine if our ray actually hits the sphere, or not. To analyse this, let's take a step back. Take a piece of paper, and draw a circle. Then, draw three lines: one missing the circle completely, one touching the sphere in exactly one point and one crossing the circle in two points. You will have something like the figure below:

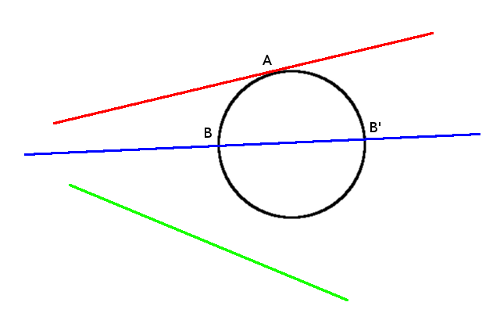
The green line misses the circle completely. The red one touches the circle in point A, while the blue line crosses the circle in point B and B'. To know if a line misses, touches or crosses a circle, we need to know some of the properties of all the actors involved. We need to know where the circle is located, how big the radius of the circle is and where the lines originate and go to. Mathematically, this is a rather trivial problem to solve. One needs the equation of the circle and the equation of the line, and check if they have any points in common by equating them.

The equation of a circle is given by (in Cartesian coordinates):

here a and b are the coordinates of the center of the circle.

The equation of a line when two points are known, can be found by solving:

This is called the two-point form of the equation of the line whereby and  are the two known points. Now, to find out where the line intersects with the circle, we can set both equal to each other. Let's put some numbers in to make it clear. Let's suppose the circle is located at (0, 0)with a radius of 5. We get for the circle:

Similarly, let's assume the two points for the line are:

When we draw this on paper with a grid, we get something like this:

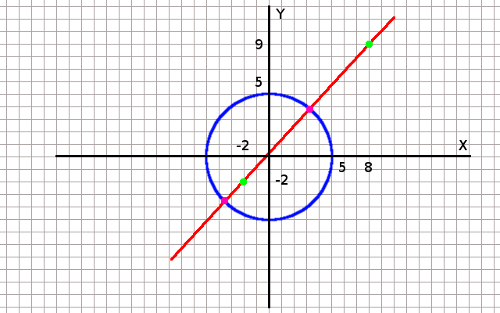
As you can see visually, the line will intersect with the circle in two points (purple colour). The known points of the line are the green ones.

To find these two points, mathematically, let's continue by filling in the knowns and simplifying:

Which becomes:

or, simplified further:

which finally leads to, solving for y:

To find where this line intersects with the circle (if at all), we can put the two equations equal. We could for example take (1.1x + 0.2), the term for y in the line equation, and put it into the circle equation substituting y, leading to:

Expanding leads  to:

Simplified this gives:

This is a quadratic equation in the its general form:

which we can solve using the quadratic formula. For this, we calclate the discriminant, defined as:

This gives us:

The fact that the solution is positive indicates that there will be two solutions. If d would have been negative, then we would have no real (only imaginary) solutions, while if d would have been 0, there would have been only one solution. This corresponds with the three possible ways we detemined the line can intersect with the circle.

Obviously, our line will intersect the circle in 2 points (which we knew from the drawing). Now we can find the solutions of the x coordinates of the points where the line intersects the circle using the discriminant in the quadratric formula as follows:

Which gives:

Which in turn gives the two solutions for x [3.26, -3.46].

For the y-coordinate we can fill in the values we just found in the equation of the the line we solved above ()

thus: 

The two intersection points of the circle and the line are thus:

(3.26, 3.786) and (-3.46, -3.606) 

You can see from the drawing that these are the correct points.

Ok, great. What does this have to do with computer graphics and ray tracing. Well, everything!

Look at the ray trace diagram all the way at the top again. Let's assume that the rays are actually x-rays and go right through the sphere. This ray will hit the sphere in either one, two or no points of the sphere, just like the line/circle calculation we just did. Think of it as if you would stick a needle and thread through a ping pong ball. Seen from the side, it looks like a circle.

Now that we know that, we can start to imagine a world where the only objects in existence are spheres. We can shoot rays at this imaginary world through a screen and check where they end up. We can adapt the line-circle intersect calculation from above to take into account the third dimension. This we will call the ray-sphere intersection calculation. 

To get to the ray-sphere intersection we need to have, again, the equation of the ray and the equation of the sphere. For the sphere, this is basically the same as the equation of the circle, but in three dimensions:

Here, as before, (a,b,c) are the coordinates of the center of the sphere and r is still the radius. The equation for a sphere centered at the origin is:

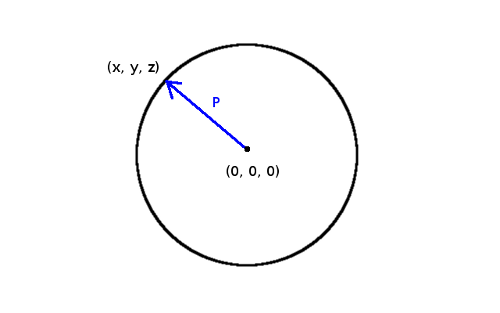
Remember the vectors we mentioned earlier?  Let's assume we have a vector denoted at (x,y,z) on the sphere and the sphere is centered at the origin:

denotes the radius, so we can state that:

Here vector multiplied with vector forms the dot product of  with  , or  . . The result of this multiplication is a scalar (in this case, ). One can easily confirm this by looking at the Pythagorean theorem. Consider the length of a vector in two dimensions, denoted as as the hypotenuse of a right triangle, then we can find this value according to the Pythagorean theorem as where x and y are the coordinates of the vector, representing the two other sides of the right triangle. The same holds true when expanding to three dimensions.

This means that the equation for a sphere centered at some arbitrary point c is:

is the subtraction of vector from vector . The resulting equation is called the implicit form of the equation of the sphere.

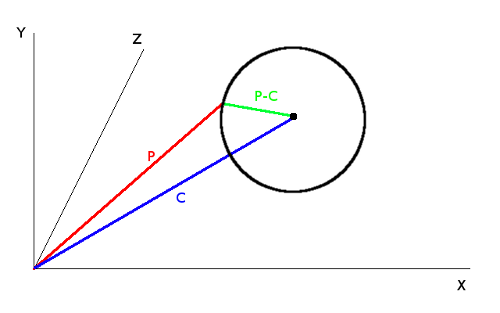
Ok, so, why switch to using vectors? The answer is because it will become a whole lot easier to work with. Let's sketch the above:

One can see two vectors in this drawing ( and ) and the difference between the two representing the radius of the sphere. The lengts of the vector  is the numerical value indicating the radius.

Besides the sphere, we also have our ray, which is basically our line from before, but then determined by two points in three-dimensional space. We can however look at it from a different perspective and say that our ray has an origin, and a direction . Both are again vectors. The nice thing we can do here is what is called parameterizing. We can represent our ray in parametrized form as follows:

In this equation, t represents a scalar parameter. Remember that ,   and are vectors represented by three coordinates, so we can see this as follows:

Let's assume for simplicity reasons that is the origin (0,0,0). We get then that:

For example, we have a ray with direction , what are some of the points that are on this vector? Answer:

etc... 

So by altering the parameter t, we find different points which are on the vector representing our ray.

What we can do next, just like when solving the line/circle intersection, is putting both equations equal. We can do this by inserting the parametrized ray equation into the implicit equation of the sphere. 

substitution gives then:

We can move to the left side of the equal sign:

Then solve the equation further by working out the multiplication (keeping in mind that , and are vectors and is a scalar) and using the distributive property of dot products to group certain parts:

This becomes:

Grouping terms and re-ordering:

Look familiar? Maybe if we make some substitutions. 

Let's make:

This makes:

That's a quadratic equation which we can solve by using the discriminant like before with the circle and line. 

We now have almost everything to write this down in code, let's try. We will write a C function called intersectRaySphere(). It will take two arguments ray and sphere and returns true if there is at least one intersection, and false when there is none.

bool intersectRaySphere(ray *r, sphere *s){

        /* A = d.d, the vector dot product of the direction */
       float A = vectorDot(&r->dir, &r->dir); 

        /* We need a vector representing the distance between the start of 
         * the ray and the position of the circle.
         * This is the term (p0 - c) 
         */
         vector dist = vectorSub(&r->start, &s->pos);

         /* 2d.(p0 - c) */  
         float B = 2 * vectorDot(&r->dir, &dist);

         /* (p0 - c).(p0 - c) - r^2 */
         float C = vectorDot(&dist, &dist) - (s->radius * s->radius);

        /* Solving the discriminant */
        float discr = B * B - 4 * A * C;

        /* If the discriminant is negative, there are no real roots.
        * Return false in that case as the ray misses the sphere.
        * Return true in all other cases (can be one or two intersections)
        */

     if(discr < 0)
         return false;
     else
         return true;
}

We can see that we are using several functions and entities we haven't seen before. The ray and sphere entities are structs which hold the appropriate parameters to define each. For the sphere, we have the following:

typedef struct{
        vector pos;
        float  radius;
}sphere; 

Similarly, the ray:

typedef struct{
        vector start;
        vector dir;
}ray;

The functions vectorSub and vectordot look like this:

/* Subtract two vectors and return the resulting vector */

vector vectorSub(vector *v1, vector *v2){
       vector result = {v1->x - v2->x, v1->y - v2->y, v1->z - v2->z };
       return result;
}

The subtraction of two vectors is very straight forward; one just subtracts the x, y, and z values of one vector from the x, y, and z values of the other.  

/* Multiply two vectors and return the resulting scalar (dot product) */

float vectorDot(vector *v1, vector *v2){
        return v1->x * v2->x + v1->y * v2->y + v1->z * v2->z;
}

The dot product takes two vectors and returns a scalar result. One needs to multiply the x, y, and z values of both vectors and add them together.

So, how do we test this and how do we use this to make pretty graphics. As a first step, let's verify that our function intersectRaySphere() actually works. The C program attached uses the functions and structures defined above to generate a 40x40 representation of a screen with a sphere somewhere in the scene. It will print some text to the console as visual verification, but in part 2 we will stick to real graphics - I promise.

Attachments

raytrace_part1.c

raytrace_part1.c 2.47 KB